Probabilistische Werkstoff- und Bauteilbewertung
Probabilistische Werkstoff- und Bauteilbewertung
Eine Bauteilbemessung wird in der ingenieurmäßigen Berechnungspraxis meist deterministisch mit den jeweils vorliegenden Werkstoffkennwerten und Belastungsszenarien durchgeführt. Die Lasten basieren dabei auf Erfahrungswerten, Messwerten oder Lastfallkatalogen, die alle möglichen Lastfälle abdecken sollen. Als Werkstoffkennwerte werden im Allgemeinen Mindestwerte aus Normen oder Messungen verwendet. Eine solche Vorgehensweise liefert als Ergebnis, ob eine Konstruktion sicher betrieben werden kann und weist ggf. einen Sicherheitsabstand aus. Dabei wird nicht berücksichtigt, dass in der Realität mit einer gewissen Wahrscheinlichkeit auch Abweichungen von den angenommenen Eingangsdaten vorliegen können. Solche Abweichungen können z.B. Streuungen der Werkstoffeigenschaften, ungeordnete Mikrostrukturen, Defekte im Werkstoff, Abweichungen in der Konstruktion, Fertigungsungänzen, unbekannte innere Spannungen wie z.B. Schweißeigenspannungen oder unvorhergesehene äußere Belastungen sein. Ziel einer probabilistischen Bauteilbewertung ist es, die Wahrscheinlichkeit des Auftretens solcher Ereignisse in der Analyse der Bauteilintegrität zu berücksichtigen und damit eine Aussage zu deren Auswirkungen auf das Bauteilverhalten bzw. zu dessen Zuverlässigkeit zu liefern. Solche Zuverlässigkeitsbetrachtungen sind für viele Produkte gerade im Hinblick auf die Risikobewertung und die Vermeidung von Gewährleistungsschäden unerlässlich.
Schwerpunkte der Forschungs- und Entwicklungsarbeiten am Fraunhofer IWM sind probabilistische Werkstoff- und Bauteilbewertungen für moderne Werkstoffe wie Faserverbundwerkstoffe, Kunststoff- oder Metallschäume, höchstfeste Stähle, Gusseisen und Stahlguss sowie Schweißverbindungen. Bei diesen Werkstoffen, die in den verschiedensten Branchen – von der Automobilindustrie über die Luft- und Raumfahrt bis zur Medizintechnik – eingesetzt werden, können sich Unterschiede in der Mikrostruktur oder vorhandene Mikro-oder Makrodefekte stark auf deren Festigkeitseigenschaften auswirken. Mit Hilfe von probabilistischen Analysen kann die heterogene Mikrostruktur mit ihrer Streuung erfasst und für Bauteile aus solchen Werkstoffen eine umfassende Sicherheits- und Zuverlässigkeitsbewertung durchgeführt werden.
Methoden/Leistungen
- Experimentelle Mikrostrukturcharakterisierung zur Ermittlung der charakteristischen Materialparameter und ihren Auftrittswahrscheinlichkeiten (z.B. Zell-/Korngrößen, Faserlängen/-orientierungen, Defekte)
- Zufallsgesteuerte Mikrostrukturgenerierung basierend auf statistisch repräsentativen Eingangsgrößen unter Berücksichtigung deren Streuung:
- Zellstrukturen (offen- /geschlossenzellig)
- Faserverstärkte Strukturen
- Kornstrukturen
- Probabilistische Homogenisierungsverfahren zur Ermittlung makroskopischer effektiver Materialeigenschaften (z.B. Steifigkeit), deren Streuung sowie der Korrelation untereinander und der räumlichen Korrelation durch Substrukturauswertung statistisch repräsentativer Volumenelemente bzw. Auswertung von Testvolumenelementen, die in ihrer Gesamtheit statistisch repräsentativ sind
- Effektive Berechnung durch gezielte Diskretisierung des Zufallsraums anstelle eines reinen Monte-Carlo-Verfahrens
- Ableitung probabilistischer Stoffgesetze sowie Algorithmen-Entwicklung zur Zufallsfelder-Generierung für probabilistische Bauteilberechnungen mit mikrostrukturellen Anteilen, die die Streuung und Korrelation der Mikrostrukturparameter berücksichtigt
- Validierung durch statische/zyklische Mikro- und Makroversuche experimentell sowie numerisch
- Ermittlung der effektiven Materialeigenschaften und Spannungs-Dehnungs-Kurven
- Lokale Dehnungsmessung, ARAMIS
- Untersuchung des Größeneffekts (effektive Materialeigenschaften streuen mehr bei kleineren Auswertebereichen)
- Bewertung von Rissinitiierung und –wachstum durch gekoppelte schädigungs- und bruchmechanische Methoden für Bauteile mit Defekten / Ungänzen
- IWM VERB - ein Softwaretool zur Beurteilung von Komponenten mit rissartigen Defekten.
- Probabilistisches Verfahren zur Ermittlung von Anrisszyklenzahlverteilungen
Multiskalige probabilistische Werkstoffmodellierung
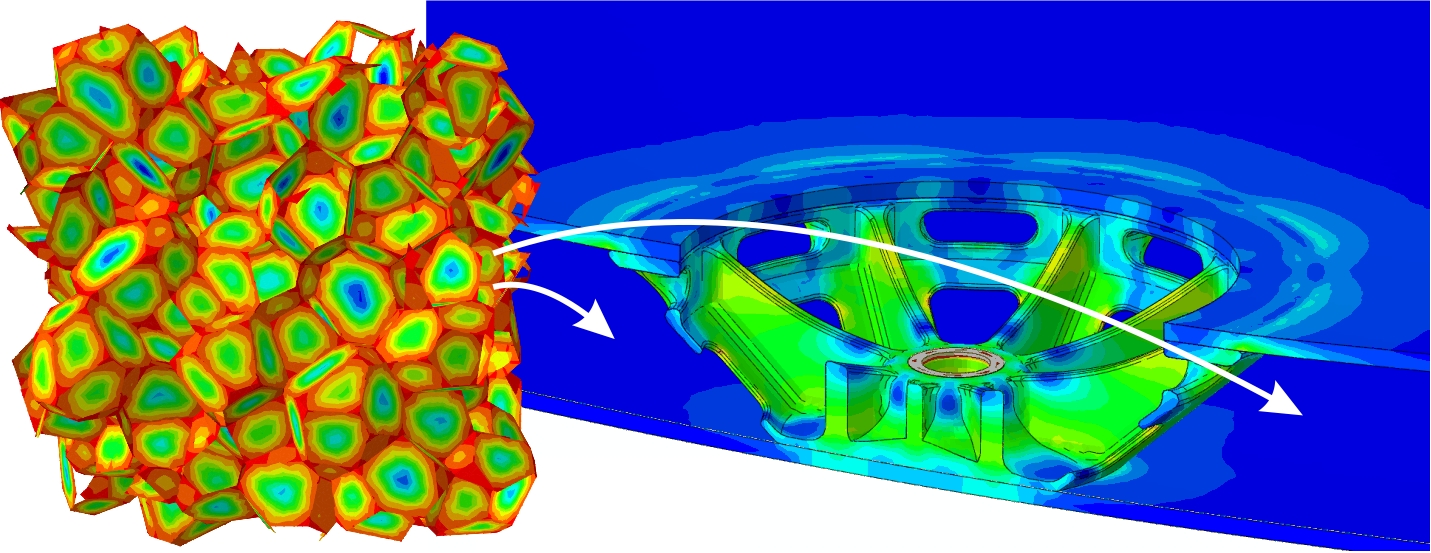
Moderne Werkstoffe wie faserverstärkte Kunststoffe, Metallschäume oder Sandwichstrukturen besitzen eine heterogene oder ungeordnete Mikrostruktur, deren stochastische Eigenschaften auf den verschiedensten Skalen rechnerisch simuliert werden können, um schließlich das gesamte Bauteilverhalten beschreiben zu können. Methodisch erfolgt die Simulation in der Regel in drei Schritten:
- 1. Simulation des stochastischen Werkstoffverhaltens auf der Mikrostrukturebene,
- 2. Homogenisierung, Ermittlung der probabilistischen, makroskopischen Materialeigenschaften,
- 3. Probabilistische Bauteilberechnung unter Berücksichtigung der stochastischen Verteilung der effektiven Materialeigenschaften.
Auf der Mikrostrukturebene werden dabei je nach Werkstoff unterschiedliche Methoden eingesetzt und weiterentwickelt. Für zelluläre Werkstoffe wie Schäume werden Größe, Form und Verteilung der Zellen in einer Struktur durch verschiedene zufallsgesteuerte Methoden wie die stochastische Variation regulärer Zellstrukturen oder Voronoi-Prozessen generiert, für faserverstärkte Kunststoffe werden Fasern und Matrixmaterial in ihrem verpressten Zustand simuliert und für partikelverstärkte Werkstoffe stehen statistische Kugel- oder Ellipsoidpackungsverfahren zur Verfügung. Generell werden die so generierten Mikrostrukturen experimentell durch Materialschliffe oder computertomographische (CT-) Verfahren und die simulierten mechanischen Eigenschaften z.B. durch Versuche an Mikroproben validiert.
Auf der Makroebene können die effektiven Materialeigenschaften durch direkte Monte-Carlo-Simulation durch Erzeugung und Analyse einer großen Zahl an statistischen Volumenelementen, durch Sampling-Methoden (Kombination von Monte-Carlo mit Analyse einer begrenzten Zahl an statistischen Volumenelementen) oder durch Substrukturmethoden ermittelt werden.
Bei der probabilistischen Bauteilberechnung schließlich wird die zufällige Verteilung der effektiven Materialeigenschaften unter Berücksichtigung aller relevanten örtlichen Eigenschaftskorrelationen und Korrelationen der einzelnen Materialparameter untereinander erfasst, über Zufallsfelder modelliert und das Bauteilverhalten in einer Monte-Carlo-Simulation analysiert.
- Beckmann, C. and Hohe, J.: Effects of material uncertainty in the structural response of metal foam core sandwich beams, Compos. Struct. 113 (2014) 382-395. Link
- Hohe, J., Beckmann, C. and Paul, H.: Modeling of uncertainties in long fiber reinforced thermoplastics, Mat. Des. 66 (2015) 390-399. Link
- Hohe, J., Paul, H. and Beckmann, C.: A probabilistic elasticity model for long fiber reinforced thermoplastics with uncertain microstructure, Mech. Mat. 122 (2018) 118-132. Link
Probabilistische Modellierung von Kunststoff und Metallschäumen
Kunststoffe oder Metallschäume werden zunehmend in Leichtbaustrukturen, z.B. im Automobilbau eingesetzt. Insbesondere Metallschäume ermöglichen eine leichte Bauweise bei vergleichbar hoher Festigkeit und großen Deformationsvermögen und sind daher besonderes als Crashelemente geeignet. Um solche Werkstoffe im Rahmen einer probabilistischen Analyse berechenbar zu machen, müssen die mechanischen Kennwerte in Form von effektiven Materialeigenschaften mit Mittelwert, Streuung und Verteilungsfunktion bekannt sein.
Hierfür werden auf der Mikrostrukturebene einerseits repräsentative Volumina betrachtet, die aus regulären Zellstrukturen bestehen und deren Zellgröße, Zellform und –verteilung stochastisch variiert wird. Andererseits stehen für die stochastische Modellierung verschiedene Voronoi-Verfahren zur Verfügung, die insgesamt die Streubreite der möglichen Mikrostrukturverteilungen und damit der Streuung der makroskopischen Materialeigenschaften abdecken. Auf der Makroebene wird das stochastische Verhalten der Bauteilkomponente dann durch direkte Monte-Carlo-Simulation durch Erzeugung und Analyse einer großen Zahl an statistischen Volumenelementen, durch Sampling-Methoden (Latin-Hypercube-Methoden oder Diskretisierung des Raums der Zufallsvariablen bei gezielter Erzeugung und Analyse einer begrenzten Zahl an statistischen Volumenelementen und Wichtung der Ergebnisse mit der Auftrittswahrscheinlichkeit der zu Grunde liegenden Mikrostruktur) oder durch Substrukturmethoden (Erzeugung eines großformatigen, statistisch repräsentativen Volumenelements mit Auswertung auf Substrukturen als statistische Volumenelemente) ermittelt.
In analoger Weise lassen sich mit diesen Methoden auch Sandwichbauteile mit einem Schaumkern berechnen.
- Beckmann, C. and Hohe, J.: Assessment of material uncertainties in solid foams based on local homogenization procedures, Int. J. Solids Struct. 49 (2012) 2807-2822. Link
- Beckmann, C. and Hohe, J.: Numerical prediction of disorder effects in solid foams using a probabilistic homogenization scheme, Mech. Mat. 78 (2014) 22-43.
- Baumeister, J., Weise, J., Hirtz, E., Höhne, K. and Hohe, J.: Applications of aluminium foam sandwiches in battery housings for electric vehicles, Mat. Sci. Eng. Tech. 45 (2014) 1099-1107. Link
- Beckmann, C. and Hohe, J.: A probabilistic constitutive model for closed-cell foams, Mech. Mat. 96 (2016) 96-105. Link
Probabilistische Mikrostrukturgenerierung und Materialmodelle für ungeordnete Faserverbunde
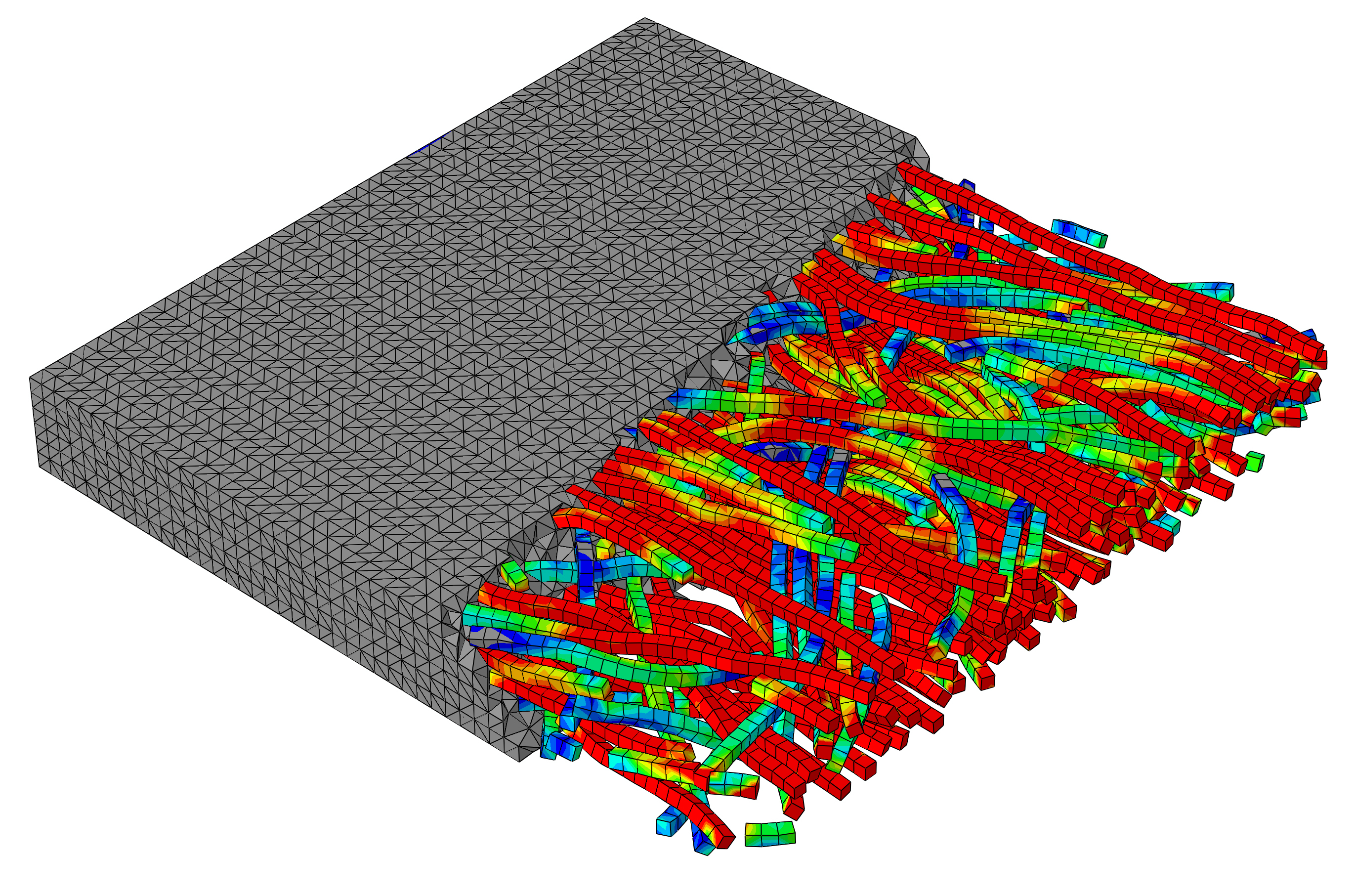
Ungeordnete Faserverbunde sind z.B. faserverstärkte Kunststoffe mit einem Duromer oder einem Thermoplast als Matrixmaterial und Kohle- oder Glasfasern als Verstärkung. Solche Werkstoffe kombinieren eine leichte Bauweise mit einer sehr hohen Festigkeit und Steifigkeit in Faserrichtung. Sie werden meist bei extremen Anforderungen, z.B. in der Luft- und Raumfahrt, im Rennsport oder der Medizintechnik eingesetzt, finden aber zunehmende Anwendung auch in anderen Bereichen wie der Automobiltechnik, der Windenergie oder auch im Schiffbau.
Als Basis für eine probabilistische Simulation wird zunächst ein Modell der Mikrostruktur im verpressten Zustand erstellt, wobei zur Bestimmung die Fasergeometrien und
-orientierungen aus Mikroschliffen abgeleitet werden. Mittels einer Miniatur- und Mikroprobenprüftechnik (Prüfquerschnitt ca. 2mm x 2mm bzw. 200µm x 200µm) werden weiterhin die Eigenschaftsvariationen über einen Array von eng beieinander liegenden Messstellen ermittelt.
Auf der Basis der Ergebnisse wird ein probabilistisches Materialmodell abgeleitet. Diese basiert auf der Einzelfaserlösung, aus der eine Lösung für das ungeordnete Mehrfaserproblem abgeleitet wird.Die stochastischen Effekte durch streuende Faserorientierung und –dichte werden durch geeignete Verteilungsfunktionen erfasst. Experimentell validiert werden die Ergebnisse durch Versuche an Standardproben mit lokaler Dehnungsmessung über ARAMIS und lokaler Auswertung der Steifigkeit. Auf diese Weise erhält man ein validiertes, probabilistisch formuliertes Materialgesetz.
- Beckmann, C. and Hohe, J.: Assessment of material uncertainties in solid foams based on local homogenization procedures, Int. J. Solids Struct. 49 (2012) 2807-2822. Link
- Fliegener, S., Luke, M. and Gumbsch, P.: 3D microstructure modeling of long fiber reinforced thermoplastics, Compos. Sci. Tech. 104 (2014) 136-145. Link
Ermüdungsverhalten und Rissentstehung bei Schweißverbindungen unter Berücksichtigung der stochastischen Mikrostruktur
Für die Auslegung von Bauteilen ist die Bewertung der Schädigungsinitiierung von ausschlaggebender Bedeutung. Insbesondere bei zyklischen Betriebsbeanspruchungen ist zu prognostizieren, ob die vorliegende Mikrostruktur weiteres Risswachstum eher begünstigt oder mindert. In Schweißverbindungen ist eine Bewertung aufgrund der prozessbedingt unterschiedlichen Gefügestrukturen besonders schwierig. Konventionell wird die Schädigungsinitiierung über Initiierungs- Wöhlerkurven experimentell ermittelt und bewertet, numerisch kann eine Rissinitiierung über Schädigungsparameter abgeschätzt werden. Diese Methoden sind aber nicht in der Lage, den Einfluss der stochastisch verteilten Mikrostruktur auf die Rissentstehung und damit deren statistisches Verhalten zu berücksichtigen.
Der Einfluss der Mikrostruktur auf das Ermüdungsverhalten wurde am Fraunhofer IWM über eine probabilistische Analyse eines Anfangsdefekts in Kornstrukturmodellen einer Schweißverbindung in Kombination mit Versuchen an Mikroproben untersucht. Dabei wurden mehrere Kornstrukturmodelle zufallsgesteuert generiert und die Rissbildungsphase mit Finite-Elemente-Berechnungen analysiert. Im Ergebnis ergibt sich eine mikrostrukturbedingte ausgeprägte Streuung in den Anriss-Zyklenzahlen, auf deren Basis ein probabilistisches Bewertungskonzept entwickelt wurde. Das neue Verfahren vermeidet unnötige Konservativitäten und liefert damit eine Verbesserung der Materialausnutzung.
- Beckmann, C., Farajian, M., Siegele, D. and Hohe, J.: Modelling and simulation of fatigue crack initiation in metallic joints based on crystal plasticity, Lett. Appl. Nano Bio Sci. 5 (2016) 354-357. Link
- Beckmann, C. and Hohe, J.: Modelling transgranular crack growth in random 3D grain structures under cyclic loading, Prob. Eng. Mech. 50 (2017) 45-52. Link
- Beckmann, C., Preußner, J., Kennerknecht, T., Farajian, M., Luke, M. and Hohe, J.: Mikrostrukturbasierte Beschreibung: Rissentstehung in Schweißverbindungen, Konstr. (2018) 64-69. Link
- Beckmann, C., Kennerknecht, T., Preußner, J., Farajian, M., Luke, M. and Hohe, J.: Micromechanical investigation and numerical simulation of fatigue crack formation in welded joints, Eng. Frac. Mech. 198 (2018) 142-157. Link
Abschätzung von Schweißeigenspannungen mittels künstlicher neuronaler Netze
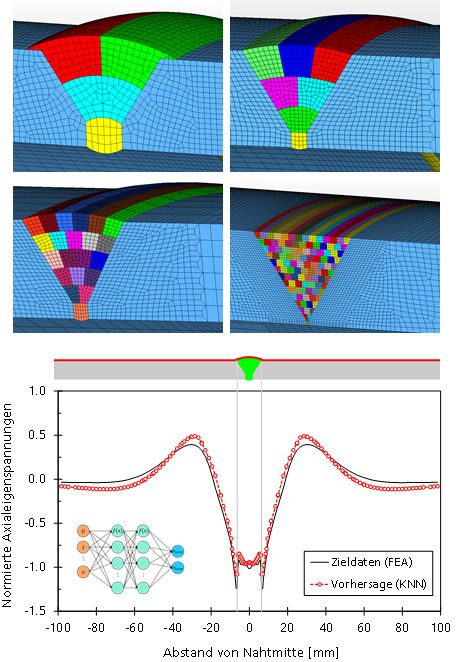
Die Genauigkeit und Treffsicherheit der probabilistischen Analysemethoden zur Bestimmung der Lebensdauer und Strukturintegrität geschweißter Bauteile hängt maßgeblich von der Höhe und Verteilung der Schweißeigenspannungen ab. Da diese in der Regel nicht bekannt sind, werden sie oft mittels konservativer Abschätzungen beschrieben, beispielsweise durch die Annahme von Zugeigenspannungen in Höhe der Streckgrenze im gesamten Einflussbereich der Schweißnaht.
Basierend auf numerischen Simulationen von Rohrschweißungen unter Variation von Wärmeeintrag, Wandstärke, Rohrdurchmesser und Anzahl der Schweißlagen wurde ein neuartiger Ansatz zur rechnerischen Abschätzung von Schweißeigenspannungen mittels künstlicher neuronaler Netze (KNN) entwickelt. Damit können die für den Ermüdungsfestigkeitsnachweis erforderlichen Schweißeigenspannungen entlang der Außen- und Innenseite eines Rohres abgeschätzt werden. Darüber hinaus liefert das KNN die für eine bruchmechanische Bewertung notwendigen Eigenspannungsprofile über der Rohrwandung im gesamten Bauteilquerschnitt.
Probabilistische bruchmechanische Bauteilbewertung
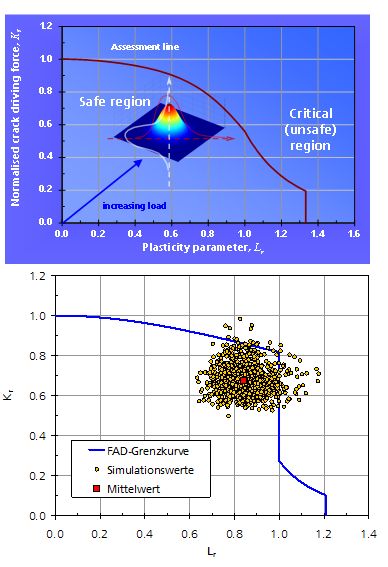
Mit bruchmechanischen Analysen wird der Einfluss von vorliegenden bzw. postulierten Fehlern auf die Festigkeit sowie die Restlebensdauer eines Bauteils bewertet. Als Fehler können dabei Mikrostrukturdefekte, Bindefehler oder Poren in Schweißverbindungen, Ungänzen in einem Gussteil, Schmiededefekte sowie infolge von Herstellung oder im Betrieb entstandene Risse betrachtet werden. Die für einen bruchmechanischen Sicherheitsnachweis erforderlichen Eingangsdaten wie die Fehler- bzw. Rissgröße und –lage, Festigkeits- und bruchmechanische Kennwerte sowie betriebliche Lasten sind oft nur näherungsweise bekannt bzw. unterliegen einer natürlichen Streuung. In einem konventionellen, deterministischen Nachweis werden alle relevanten Eingangsgrößen als konservativ abgeschätzte Grenzwerte in der Bewertung berücksichtigt. Da jedoch solche Grenzwerte in der Realität nur selten bzw. nicht für alle Kenngrößen vorliegen, werden im Rahmen des deterministischen Nachweises nach einem jeweils anzuwenden Regelwerk zusätzliche Sicherheitsfaktoren verwendet. Die daraus resultierende Bewertung kann zu sehr konservativen bzw. unrealistischen Ergebnissen und somit zu einer falschen Einschätzung der technischen Sicherheit und der Verfügbarkeit eines Bauteils führen.
Im Rahmen einer probabilistischen Nachweisführung werden Ist-Werte der Eingabegrößen als statistische Verteilungen verwendet und als Ergebnis die Versagenswahrscheinlichkeit des Bauteils bzw. die Wahrscheinlichkeitsverteilung der Restlebensdauer ermittelt. Ein wesentlicher Vorteil des probabilistischen Ansatzes besteht darin, dass die Streuungen aller Kenngrößen (Beanspruchungs-, Werkstoff- und Fehlerzustand) gleichzeitig berücksichtigt werden können und damit eine realitätsnahe Beschreibung der Versagenswahrscheinlichkeit ohne zusätzlichen Gebrauch von Sicherheitsfaktoren möglich ist. Darüber hinaus lassen sich probabilistische Methoden in moderne Strategiepläne für die Festlegung von Inspektionsmaßnamen sowie Lebensdauermanagement integrieren.
Probabilistische bruchmechanische Ansätze sind in der gegenwärtigen Fassung der FKM-Richtlinie „Bruchmechanischer Festigkeitsnachweis für Maschinenbauteile“ beschrieben und im Fehlerbewertungsprogramm IWM VERB enthalten. Die Berechnung der Versagenswahrscheinlichkeiten kann dabei wahlweise mit der klassischen Monte-Carlo-Simulation oder mit einer rechnerisch effizienteren Zuverlässigkeitsmethode, u.a. FORM, SORM oder Sampling-Verfahren, erfolgen. Des Weiteren stehen in IWM-VERB verschiedene Tools für die statistische Datenanpassung und die Bewertung der Anpassungsgüte zur Verfügung.
Publikationen
- Hohe, J., Geometry modelling and elastic property prediction for short fiber composites, Multi-scale continuum mechanics modelling of fibre-reinforced polymer composites, Part I: Geometry construction and homogenization of linear elastic material behavior at micro- and meso-scale; van Paepegem, W. (Ed.); Elsevier B.V., Amsterdam, NL (2021) 55-77 Link
- Radaelli, F.; Amann, C.; Aydin, A.; Varfolomeev, I.; Gumbsch, P.; Kadau, K., A probabilistic model for forging flaw crack nucleation processes, Proc. of ASME Turbo Expo: Power for Land, Sea, and Air 2020, Vol. 10B/Structures an Dynamics; American Society of Mechanical Engineers (ASME), New York, NY, USA (2021) Paper No: GT2020-14606, V10BT28A004; 10 pages Link
- Hohe, J.; Beckmann, C.; Böhme, W.; Weise, J.; Reinfried; M.; Luthardt, F.; Rapp, F.; Diemert, J., An experimental and numerical survey into the potential of hybrid foams, Mechanics of Materials 136 (2019) 103063 1-15 Link
- Zerbst, U.; Madia, M.; Schork, B.; Hensel, J.; Kucharczyk, P.; Ngoula, D.; Tchuindjang, D.; Bernhard, J.; Beckmann, C., Fatigue and fracture of weldments - The IBESS approach for the determination of the fatigue life and strength of weldments by fracture mechanics analysis; Springer Nature Switzerland AG, Cham, Schweiz (2019) 157 Seiten Link
- Beckmann, C.; Kennerknecht, T.; Preußner, J.; Farajian, M.; Luke, M.; Hohe, J., Micromechanical investigation and numerical simulation of fatigue crack formation in welded joints, Engineering Fracture Mechanics 198 (2018) 142-157 Link
- Hohe, J.; Paul, H.; Beckmann, C., A probabilistic elasticity model for long fiber reinforced thermoplastics with uncertain microstructure, Mechanics of Materials 122 (2018) 118-132 Link
 Fraunhofer-Institut für Werkstoffmechanik IWM
Fraunhofer-Institut für Werkstoffmechanik IWM